Calcul de l’écart de fermeture angulaire
Comprendre le Calcul de l’écart de fermeture angulaire
Vous êtes un géomètre chargé de vérifier la précision d’un levé topographique pour un nouveau développement urbain.
Le périmètre du terrain forme un polygone fermé, et vous devez calculer l’écart de fermeture angulaire pour assurer que les mesures prises sont précises.
Pour comprendre le Calcul de la Fermeture Angulaire, cliquez sur le lien.
Données:
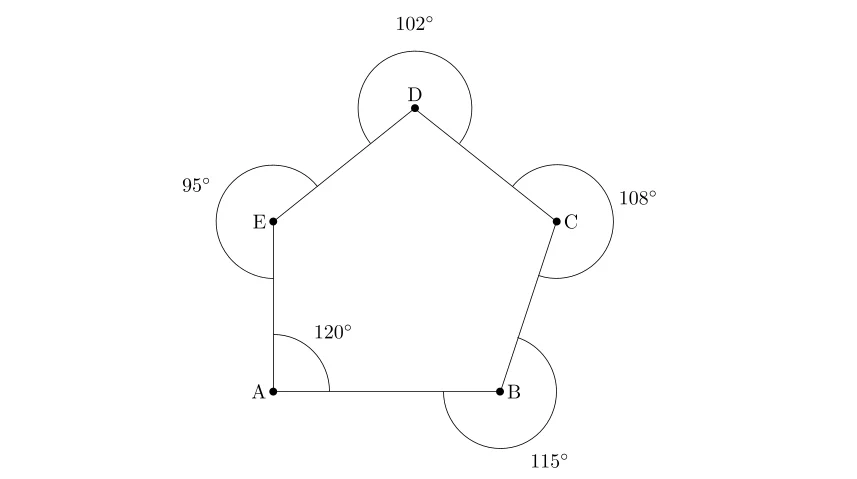
Le périmètre du terrain est divisé en 5 points de stationnement, formant un pentagone. Les angles internes mesurés au niveau de chaque point sont les suivants:
Point A: \(120^\circ\)
Point B: \(115^\circ\)
Point C: \(108^\circ\)
Point D: \(102^\circ\)
Point E: \(95^\circ\)
Questions:
1. Calculer l’écart de fermeture angulaire.
2. Analyse de l’écart:
Déterminez si l’écart de fermeture angulaire est acceptable selon les normes de précision topographique. Les normes typiques permettent un écart de 0.3° par angle pour un levé de précision moyenne.
3. Discussion:
Quelles pourraient être les causes d’un écart inacceptable et comment peut-on les corriger lors de futurs levés ?
Correction : Calcul de l’écart de fermeture angulaire
1. Calcul de l’écart de fermeture angulaire
Calcul théorique:
Pour un pentagone, la somme des angles internes, \(S_{\text{théorique}}\), se calcule par la formule:
\[ S_{\text{théorique}} = (n-2) \times 180^\circ \]
où \(n = 5\) (le nombre de côtés du polygone).
Calcul:
\[ S_{\text{théorique}} = (5-2) \times 180^\circ \] \[ S_{\text{théorique}} = 3 \times 180^\circ \] \[ S_{\text{théorique}} = 540^\circ \]
Calcul mesuré:
La somme des angles internes mesurés, \(S_{\text{mesurée}}\), est la somme des angles donnés:
\[ S_{\text{mesurée}} = 120^\circ + 115^\circ + 108^\circ + 102^\circ + 95^\circ \]
Calcul:
\[ S_{\text{mesurée}} = 540^\circ \]
Écart de fermeture angulaire
L’écart de fermeture angulaire, \(\Delta\), est calculé comme la différence entre la somme théorique et la somme mesurée:
\[ \Delta = S_{\text{théorique}} – S_{\text{mesurée}} \] \[ \Delta = 540^\circ – 540^\circ \] \[ \Delta = 0^\circ \]
2. Analyse de l’écart
Résultat de l’écart : \(\Delta = 0^\circ\)
- Interprétation :
Un écart de \(0^\circ\) indique que les mesures sont extrêmement précises et qu’il n’y a pas d’erreurs de mesure significatives.
- Acceptabilité :
Selon les normes topographiques, un écart de \(0.3^\circ\) par angle est acceptable. Ici, l’écart étant de \(0^\circ\), il est largement dans les limites acceptables.
3. Discussion sur les causes potentielles d’écarts et mesures correctives
- Causes potentielles d’un écart :
- Erreurs d’observation dues à des conditions météorologiques défavorables.
- Inexactitude dans la calibration des instruments de mesure.
- Erreurs humaines dans la lecture des instruments.
- Mesures correctives :
- Réaliser des calibrations périodiques des instruments.
- S’assurer que les mesures sont prises dans de bonnes conditions environnementales.
- Former et sensibiliser le personnel aux techniques de mesure précises.
Conclusion
Les résultats montrent une précision impeccable dans le levé topographique. Cet exercice illustre l’importance de la précision des mesures et de l’adhésion stricte aux protocoles de mesure pour assurer l’intégrité des projets de développement urbain.
La maintenance régulière des équipements et la formation continue du personnel sont essentielles pour maintenir cette qualité de mesure.
Calcul de l’écart de fermeture angulaire
D’autres exercices de topographie:














0 commentaires