Calcul de la Hauteur d’une Pente
Comprendre le Calcul de la Hauteur d’une Pente
Dans le cadre d’un projet d’aménagement paysager, une entreprise de terrassement souhaite installer une série de terrasses sur une pente naturelle pour la culture de plantes ornementales. Le but de cet exercice est de calculer la hauteur de la pente nécessaire pour garantir une structure stable et efficace pour les terrasses prévues. Les terrasses devront avoir des hauteurs égales et être adaptées au type de sol et à l’inclinaison du terrain.
Pour comprendre le Calcul de Pente en Terrassement, cliquez sur le lien.
Données Fournies:
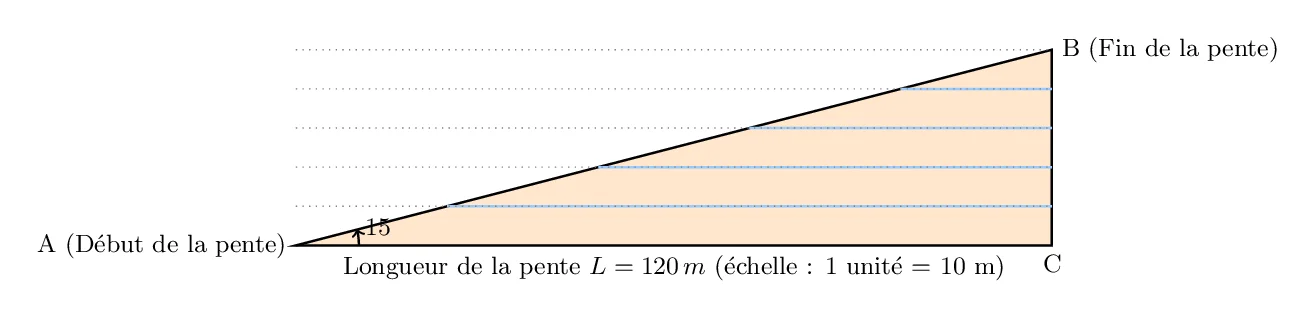
- Longueur de la pente (L) : 120 mètres
- Inclinaison de la pente (α) : 15°
- Nombre de terrasses (n) : 5
- Coefficient de sécurité (C) : 1.25 (utilisé pour assurer la stabilité des terrasses contre le glissement)
Questions:
Calculer la hauteur de chaque terrasse (h) en tenant compte du coefficient de sécurité. Vous utiliserez les relations trigonométriques et la géométrie pour déterminer la hauteur nécessaire pour que chaque terrasse respecte l’inclinaison et la longueur totale de la pente.
Correction : Calcul de la Hauteur d’une Pente
1. Calcul de la hauteur totale de la pente
La pente forme l’hypoténuse d’un triangle rectangle dont la hauteur (la différence verticale totale) se calcule à l’aide de la fonction sinus.
Formule :
\[ H_{\text{total}} = L \times \sin(\alpha) \]
Données :
- \(L = 120 \, \text{m}\)
- \(\alpha = 15^\circ\)
Calcul :
\[ H_{\text{total}} = 120 \times \sin(15^\circ) \]
En sachant que \(\sin(15^\circ) \approx 0.2588\), on obtient :
\[ H_{\text{total}} \approx 120 \times 0.2588 \] \[ H_{\text{total}} \approx 31.06 \, \text{m} \]
2. Calcul de la hauteur théorique de chaque terrasse
Si l’on répartit uniformément la hauteur totale sur le nombre de terrasses, la hauteur théorique de chaque terrasse est obtenue en divisant \(H_{\text{total}}\) par le nombre de terrasses \(n\).
Formule :
\[ h_{\text{th}} = \frac{H_{\text{total}}}{n} \]
Données :
- \(H_{\text{total}} \approx 31.06 \, \text{m}\)
- \(n = 5\)
Calcul :
\[ h_{\text{th}} \approx \frac{31.06}{5} \approx 6.21 \, \text{m} \]
3. Incorporation du coefficient de sécurité
Le coefficient de sécurité permet de réduire la hauteur de chaque terrasse pour garantir une stabilité accrue et prévenir tout risque de glissement. Pour intégrer ce coefficient, on divise la hauteur théorique par \(C\).
Formule :
\[ h = \frac{h_{\text{th}}}{C} \]
Données :
- \(h_{\text{th}} \approx 6.21 \, \text{m}\)
- \(C = 1.25\)
Calcul :
\[ h \approx \frac{6.21}{1.25} \approx 4.97 \, \text{m} \]
Conclusion
En tenant compte du coefficient de sécurité, la hauteur de chaque terrasse est d’environ 4.97 mètres (que l’on peut arrondir à 5 m).
Calcul de la Hauteur d’une Pente
D’autres exercices de terrassement:















0 commentaires