Fondations pour un bâtiment résidentiel
Comprendre le calcul sur les fondations pour un bâtiment résidentiel :
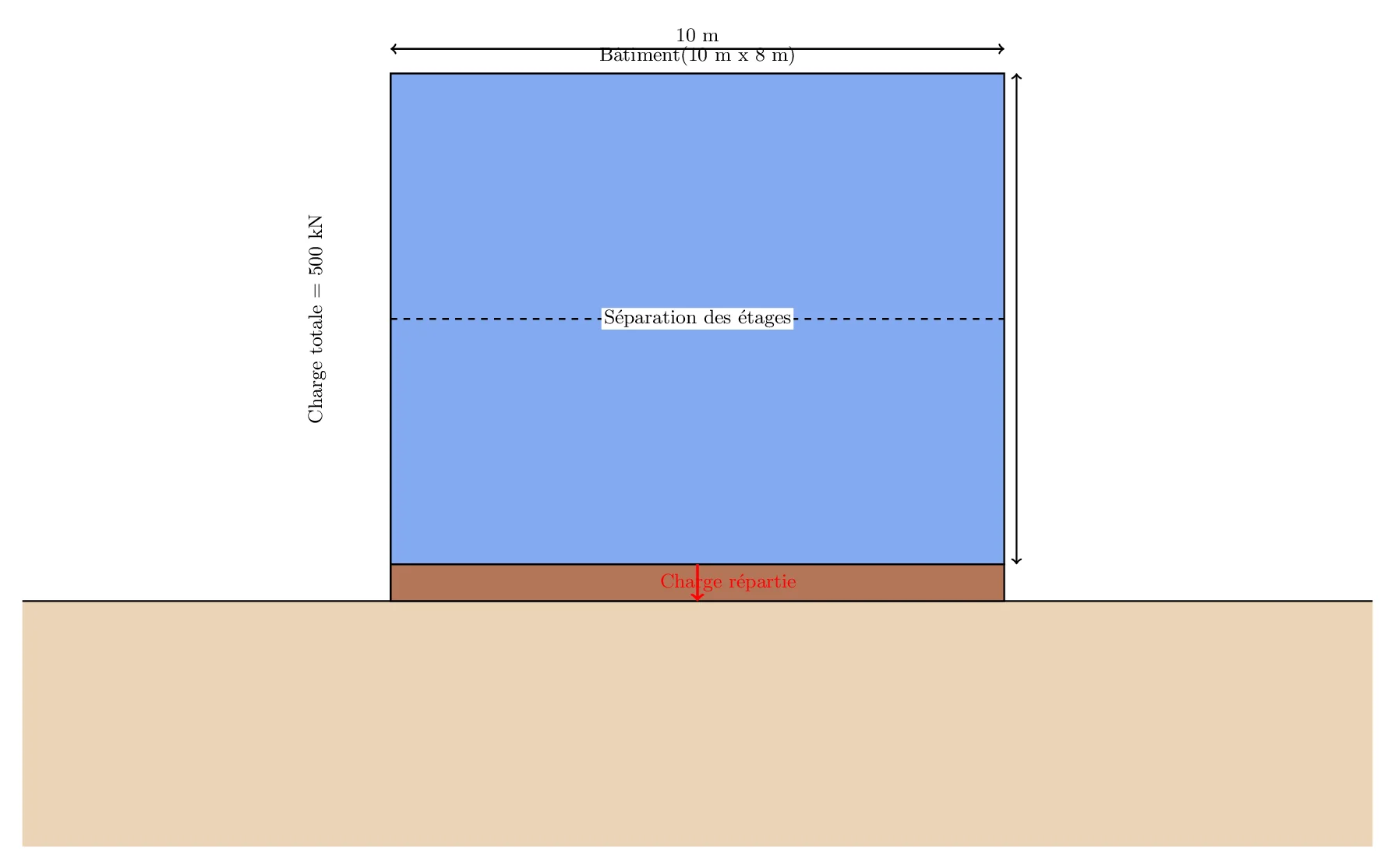
Vous êtes chargé de concevoir les fondations pour un petit bâtiment résidentiel. Le bâtiment est rectangulaire, mesurant 10 m de long et 8 m de large.
Le sol est composé d’un sol argileux, avec une capacité portante de 150 kN/m². Le bâtiment aura deux étages, avec un poids total estimé (y compris son propre poids) de 500 kN.
Pour comprendre le calcul de la Capacité Portante d’une Semelle Isolée, cliquez sur le lien.
Questions:
- Calcul de la Charge Totale : Estimer la charge totale que les fondations doivent supporter.
- Dimensionnement des Fondations : Déterminer les dimensions minimales des fondations pour répartir cette charge sans dépasser la capacité portante du sol.
Hypothèses
- Le poids propre du bâtiment est uniformément réparti.
- Les fondations sont de type semelle continue sous chaque mur porteur.
- Les murs porteurs sont disposés aux périmètres du bâtiment.
Correction : fondations pour un bâtiment résidentiel
1. Charge Totale
La charge totale donnée est de 500 kN.
2. Dimensionnement des Fondations
Surface de Contact Totale Nécessaire:
\begin{equation}
\text{S} = \frac{\text{Poids Total}}{\text{Capacité Portante}} \end{equation} \begin{equation}
\text{S} = \frac{500 \text{ kN}}{150 \text{ kN/m}^2} \approx 3.33 \text{ m}^2
\end{equation}
Toutefois, la répartition de cette surface sous chaque mur doit être précisée.
Répartition de la Charge:
Supposons que la structure est symétrique et que chaque mur porteur supporte une charge proportionnelle à sa longueur.
Charge supportée par les murs de 10 m:
\[ = \frac{10 \text{ m}}{10 \text{ m} + 10 \text{ m} + 8 \text{ m} + 8 \text{ m}} \times 500 \text{ kN} \] \[ = \frac{10}{36} \times 500 \text{ kN} \] \[ \approx 139 \text{ kN} \]
Charge supportée par les murs de 8 m:
\begin{equation}
= \frac{8 \text{ m}}{36 \text{ m}} \times 500 \text{ kN} \end{equation} \begin{equation} \approx 111 \text{ kN}
\end{equation}
Calcul des Largeurs des Fondations pour Chaque Mur:
Pour un mur de 10 m:
- Largeur de la Fondation
\begin{equation} = \frac{139 \text{ kN}}{10 \text{ m} \times 150 \text{ kN/m}^2} \end{equation} \begin{equation} \approx 0.093 \text{ m}
\end{equation}
Pour un mur de 8 m:
- Largeur de la Fondation
\begin{equation} = \frac{111 \text{ kN}}{8 \text{ m} \times 150 \text{ kN/m}^2} \end{equation} \begin{equation} \approx 0.093 \text{ m}
\end{equation}
Conclusion
Les fondations sous les murs de 10 m et 8 m devraient avoir une largeur d’au moins 0.093 m (9.3 cm) pour supporter en toute sécurité le poids estimé du bâtiment, en tenant compte de la capacité portante du sol.
Remarques Importantes
Ce calcul est une simplification et ne remplace pas une analyse détaillée par un professionnel. La répartition de la charge peut varier selon la conception structurelle spécifique du bâtiment.
D’autres facteurs comme les charges dynamiques, les conditions hydrologiques et les normes de construction locales doivent être pris en compte.
Fondations pour un bâtiment résidentiel
D’autres exercices de fondation :
0 commentaires