Charge Thermique d’un Mur Exposé au Sud
Comprendre la Charge Thermique d’un Mur Exposé au Sud
Vous êtes un ingénieur thermique chargé d’évaluer l’efficacité énergétique des matériaux utilisés dans la construction d’un nouveau bâtiment scolaire situé dans une région au climat tempéré.
Le bâtiment utilise des murs en béton avec un revêtement extérieur en brique et une isolation en laine de roche.
Vous devez déterminer la quantité totale de chaleur absorbée par un mur exposé au sud pendant une journée d’été typique.
Données Fournies:
– Dimensions du mur : 10 m de largeur x 3 m de hauteur.
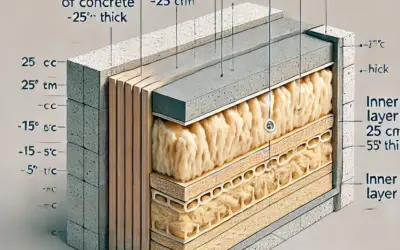
– Composition du mur :
- Brique (épaisseur 0.1 m, conductivité thermique \(k = 0.7 \, \text{W/m}\cdot\text{K}\))
- Laine de roche (épaisseur 0.2 m, conductivité thermique \(k = 0.04 \, \text{W/m}\cdot\text{K}\))
- Béton (épaisseur 0.2 m, conductivité thermique \(k = 1.7 \, \text{W/m}\cdot\text{K}\))
– Température extérieure moyenne : 35°C
– Température intérieure moyenne : 22°C
– Coefficient de transfert thermique par convection :
- Extérieur: \(h_{\text{ext}} = 25 \, \text{W/m}^2\cdot\text{K}\)
- Intérieur: \(h_{\text{int}} = 8 \, \text{W/m}^2\cdot\text{K}\)
– Irradiance solaire moyenne sur la surface exposée au sud : \(800 \, \text{W/m}^2\)
Question :
1. Calculez la résistance thermique totale du mur.
2. Déterminez le flux de chaleur à travers le mur dû à la différence de température.
3. Évaluez la quantité totale de chaleur absorbée par le mur sur une période de 12 heures, en tenant compte de l’irradiance solaire.
Correction : Charge Thermique d’un Mur Exposé au Sud
1. Calcul de la Résistance Thermique Totale du Mur
Pour calculer la résistance thermique totale, nous additionnons les résistances de chaque matériau ainsi que les résistances dues à la convection à l’intérieur et à l’extérieur.
Résistance des matériaux :
Brique:
- Épaisseur (\(d\)): 0.1 m
- Conductivité thermique (\(k\)): 0.7 \( \text{W/m}\cdot\text{K} \)
\[ R_{\text{brique}} = \frac{0.1}{0.7} \] \[ R_{\text{brique}} \approx 0.143 \, \text{m}^2\cdot\text{K/W} \]
Laine de roche:
- Épaisseur: 0.2 m
- Conductivité thermique: 0.04 \( \text{W/m}\cdot\text{K} \)
\[ R_{\text{laine}} = \frac{0.2}{0.04} \] \[ R_{\text{laine}} = 5 \, \text{m}^2\cdot\text{K/W} \]
Béton:
- Épaisseur: 0.2 m
- Conductivité thermique: 1.7 \( \text{W/m}\cdot\text{K} \)
\[ R_{\text{béton}} = \frac{0.2}{1.7} \] \[ R_{\text{béton}} \approx 0.118 \, \text{m}^2\cdot\text{K/W} \]
Résistances de convection :
Extérieur:
- Coefficient de transfert thermique: 25 \( \text{W/m}^2\cdot\text{K} \)
\[ R_{\text{conv, ext}} = \frac{1}{25 \times 30} \] \[ R_{\text{conv, ext}} = 0.00133 \, \text{m}^2\cdot\text{K/W} \]
Intérieur:
- Coefficient de transfert thermique: 8 \( \text{W/m}^2\cdot\text{K} \)
\[ R_{\text{conv, int}} = \frac{1}{8 \times 30} \] \[ R_{\text{conv, int}} = 0.00417 \, \text{m}^2\cdot\text{K/W} \]
Résistance thermique totale :
\[ R_{\text{tot}} = 0.143 + 5 + 0.118 + 0.00133 + 0.00417 \] \[ R_{\text{tot}} \approx 5.266 \, \text{m}^2\cdot\text{K/W} \]
2. Calcul du Flux de Chaleur à Travers le Mur
Différence de température (\(\Delta T\)) :
- Extérieure: 35°C
- Intérieure: 22°C
\[ \Delta T = 35 – 22 \] \[ \Delta T = 13 \, \text{K} \]
Flux de chaleur :
\[ \dot{Q} = \frac{13}{5.266} \] \[ \dot{Q} \approx 2.47 \, \text{W/m}^2 \]
Flux de chaleur total :
\[ \dot{Q}_{\text{total}} = 2.47 \times 30 \] \[ \dot{Q}_{\text{total}} = 74.1 \, \text{W} \]
3. Quantité Totale de Chaleur Absorbée par le Mur
- Durée d’exposition solaire : 12 heures (43200 secondes)
Chaleur due au flux de chaleur :
\[ Q = 74.1 \times 43200 \] \[ Q = 3,201,120 \, \text{J} \]
Chaleur due à l’irradiance solaire :
\[ Q_{\text{solaire}} = 800 \times 30 \times 43200 \] \[ Q_{\text{solaire}} = 1,036,800,000 \, \text{J} \]
Total de chaleur absorbée :
\[ Q_{\text{totale}} = 3,201,120 + 1,036,800,000 \] \[ Q_{\text{totale}} \approx 1,040,001,120 \, \text{J} \]
Conclusion
Le mur absorbe environ 1,040,001,120 Joules de chaleur sur une période de 12 heures pendant une journée d’été typique, considérant à la fois le transfert de chaleur à travers le mur et l’irradiance solaire.
Cette analyse détaille le processus de calcul et montre l’importance de l’isolation et de la gestion thermique dans la construction de bâtiments.
Charge Thermique d’un Mur Exposé au Sud
D’autres exercices de thermique des batiments:














0 commentaires