Études de cas pratique

EGC

Caractéristiques mécaniques du bois

Caractéristiques Mécaniques du Bois

Caractéristiques Mécaniques du Bois

Comprendre les Caractéristiques Mécaniques du Bois

Le bois est un matériau naturel dont les propriétés mécaniques varient en fonction de son essence, de sa densité, de son taux d'humidité, et de la présence de singularités (nœuds, fentes, etc.). Pour les calculs de structure, on utilise des valeurs caractéristiques de résistance et de rigidité, qui sont ensuite ajustées par des coefficients pour obtenir des valeurs de calcul. Ces valeurs permettent de dimensionner les éléments en bois pour qu'ils résistent aux charges appliquées (État Limite Ultime - ELU) et ne se déforment pas excessivement (État Limite de Service - ELS).

Données de l'étude

On considère un bois résineux de classe de résistance C24.

Valeurs caractéristiques pour le bois C24 (selon Eurocode 5 ou tables usuelles) :

  • Résistance caractéristique en flexion (\(f_{m,k}\)) : \(24 \, \text{MPa}\)
  • Résistance caractéristique en traction axiale (\(f_{t,0,k}\)) : \(14 \, \text{MPa}\)
  • Résistance caractéristique en compression axiale (\(f_{c,0,k}\)) : \(21 \, \text{MPa}\)
  • Résistance caractéristique au cisaillement (\(f_{v,k}\)) : \(4.0 \, \text{MPa}\)
  • Module d'élasticité moyen axial (\(E_{0,mean}\)) : \(11000 \, \text{MPa}\)

Coefficients pour le calcul des résistances de calcul :

  • Coefficient de modification (\(k_{mod}\)) : \(0.8\) (correspondant à une classe de service 1 ou 2 et une classe de durée de charge de type "Moyenne durée", par exemple pour des charges d'exploitation de plancher ou de la neige).
  • Coefficient partiel de sécurité pour le matériau bois (\(\gamma_M\)) : \(1.3\)
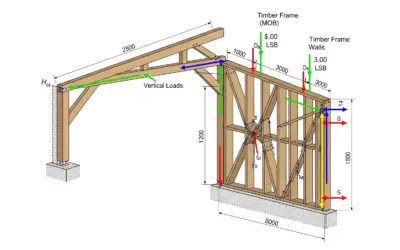
Schéma : Sollicitations Types sur une Pièce de Bois
Flexion (fm,k) Traction (ft,0,k) Compression (fc,0,k) Cisaillement (fv,k)

Illustration des différentes sollicitations et résistances caractéristiques du bois.

Questions à traiter

  1. Définir brièvement ce que représente une "résistance caractéristique" (ex: \(f_{m,k}\)).
  2. Calculer la résistance de calcul en flexion (\(f_{m,d}\)). On supposera \(k_h=1.0\) et \(k_{crit}=1.0\).
  3. Calculer la résistance de calcul en traction axiale (\(f_{t,0,d}\)).
  4. Calculer la résistance de calcul en compression axiale (\(f_{c,0,d}\)).
  5. Calculer la résistance de calcul au cisaillement (\(f_{v,d}\)).
  6. Expliquer pourquoi il est nécessaire d'utiliser un coefficient de modification \(k_{mod}\) et un coefficient partiel de sécurité \(\gamma_M\) pour passer des valeurs caractéristiques aux valeurs de calcul.

Correction : Caractéristiques Mécaniques du Bois

Question 1 : Définition d'une Résistance Caractéristique

Principe :

Une résistance caractéristique (notée avec l'indice \(k\), par exemple \(f_{m,k}\) pour la flexion) est une valeur de résistance du matériau qui a une probabilité spécifiée (généralement 95%) d'être dépassée. Autrement dit, c'est une valeur qui correspond au fractile 5% de la distribution statistique des résistances du matériau. Elle est déterminée à partir d'essais en laboratoire sur des éprouvettes et sert de base pour les calculs de dimensionnement.

Résultat Question 1 : Une résistance caractéristique est une valeur de résistance du matériau qui est attendue d'être dépassée par 95% des échantillons de ce matériau. C'est une valeur prudente utilisée comme point de départ pour les calculs de sécurité.

Question 2 : Résistance de Calcul en Flexion (\(f_{m,d}\))

Principe :

La résistance de calcul en flexion (\(f_{m,d}\)) est la contrainte que le bois peut supporter en flexion à l'ELU. Elle est obtenue en ajustant la résistance caractéristique en flexion (\(f_{m,k}\)) avec le coefficient de modification (\(k_{mod}\)) et en la divisant par le coefficient partiel de sécurité (\(\gamma_M\)). Les coefficients \(k_h\) et \(k_{crit}\) sont pris égaux à 1.0 comme indiqué.

Formule(s) utilisée(s) (Eurocode 5) :
\[f_{m,d} = k_{mod} \cdot k_h \cdot k_{crit} \cdot \frac{f_{m,k}}{\gamma_M}\]
Données spécifiques :
  • \(k_{mod} = 0.8\)
  • \(k_h = 1.0\)
  • \(k_{crit} = 1.0\)
  • \(f_{m,k} = 24 \, \text{MPa}\) (pour C24)
  • \(\gamma_M = 1.3\)
Calcul :
\[ \begin{aligned} f_{m,d} &= 0.8 \times 1.0 \times 1.0 \times \frac{24 \, \text{MPa}}{1.3} \\ &= 0.8 \times \frac{24}{1.3} \, \text{MPa} \\ &\approx 0.8 \times 18.4615 \, \text{MPa} \\ &\approx 14.769 \, \text{MPa} \end{aligned} \]
Résultat Question 2 : La résistance de calcul en flexion est \(f_{m,d} \approx 14.77 \, \text{MPa}\).

Question 3 : Résistance de Calcul en Traction Axiale (\(f_{t,0,d}\))

Principe :

La résistance de calcul en traction parallèle aux fibres (\(f_{t,0,d}\)) est calculée de manière similaire à la résistance en flexion, en utilisant la résistance caractéristique en traction axiale (\(f_{t,0,k}\)).

Formule(s) utilisée(s) (Eurocode 5) :
\[f_{t,0,d} = k_{mod} \cdot \frac{f_{t,0,k}}{\gamma_M}\]

(Les coefficients \(k_h\) et \(k_{crit}\) ne s'appliquent généralement pas directement à la traction axiale de la même manière qu'à la flexion).

Données spécifiques :
  • \(k_{mod} = 0.8\)
  • \(f_{t,0,k} = 14 \, \text{MPa}\) (pour C24)
  • \(\gamma_M = 1.3\)
Calcul :
\[ \begin{aligned} f_{t,0,d} &= 0.8 \times \frac{14 \, \text{MPa}}{1.3} \\ &\approx 0.8 \times 10.769 \, \text{MPa} \\ &\approx 8.615 \, \text{MPa} \end{aligned} \]
Résultat Question 3 : La résistance de calcul en traction axiale est \(f_{t,0,d} \approx 8.62 \, \text{MPa}\).

Question 4 : Résistance de Calcul en Compression Axiale (\(f_{c,0,d}\))

Principe :

La résistance de calcul en compression parallèle aux fibres (\(f_{c,0,d}\)) est calculée en utilisant la résistance caractéristique en compression axiale (\(f_{c,0,k}\)).

Formule(s) utilisée(s) (Eurocode 5) :
\[f_{c,0,d} = k_{mod} \cdot \frac{f_{c,0,k}}{\gamma_M}\]
Données spécifiques :
  • \(k_{mod} = 0.8\)
  • \(f_{c,0,k} = 21 \, \text{MPa}\) (pour C24)
  • \(\gamma_M = 1.3\)
Calcul :
\[ \begin{aligned} f_{c,0,d} &= 0.8 \times \frac{21 \, \text{MPa}}{1.3} \\ &\approx 0.8 \times 16.154 \, \text{MPa} \\ &\approx 12.923 \, \text{MPa} \end{aligned} \]
Résultat Question 4 : La résistance de calcul en compression axiale est \(f_{c,0,d} \approx 12.92 \, \text{MPa}\).

Question 5 : Résistance de Calcul au Cisaillement (\(f_{v,d}\))

Principe :

La résistance de calcul au cisaillement (\(f_{v,d}\)) est calculée en utilisant la résistance caractéristique au cisaillement (\(f_{v,k}\)).

Formule(s) utilisée(s) (Eurocode 5) :
\[f_{v,d} = k_{mod} \cdot \frac{f_{v,k}}{\gamma_M}\]
Données spécifiques :
  • \(k_{mod} = 0.8\)
  • \(f_{v,k} = 4.0 \, \text{MPa}\) (pour C24)
  • \(\gamma_M = 1.3\)
Calcul :
\[ \begin{aligned} f_{v,d} &= 0.8 \times \frac{4.0 \, \text{MPa}}{1.3} \\ &\approx 0.8 \times 3.077 \, \text{MPa} \\ &\approx 2.462 \, \text{MPa} \end{aligned} \]
Résultat Question 5 : La résistance de calcul au cisaillement est \(f_{v,d} \approx 2.46 \, \text{MPa}\).

Question 6 : Influence de \(k_{mod}\) et \(\gamma_M\)

Explication :

Les valeurs caractéristiques des résistances du bois (\(f_k\)) sont des valeurs statistiques obtenues en laboratoire dans des conditions idéales (souvent pour des charges de courte durée et une humidité contrôlée).

  • Coefficient de modification (\(k_{mod}\)) : Ce coefficient ajuste la résistance caractéristique pour tenir compte des conditions réelles d'utilisation qui peuvent affecter la résistance du bois. Les deux principaux facteurs pris en compte par \(k_{mod}\) sont :
    • La classe de service : Elle reflète l'humidité ambiante à laquelle le bois sera exposé (Classe 1 pour intérieur sec, Classe 2 pour intérieur humide ou extérieur abrité, Classe 3 pour extérieur exposé). Une humidité plus élevée tend à réduire la résistance du bois.
    • La durée de la charge : Le bois peut supporter des charges plus importantes pendant de courtes périodes que pendant de longues périodes (phénomène de fluage et de fatigue). \(k_{mod}\) est donc plus faible pour les charges de longue durée (ex: poids propre) que pour les charges de courte durée (ex: vent).
    • Dans cet exercice, \(k_{mod} = 0.8\) indique des conditions qui réduisent la résistance par rapport aux conditions de référence (par exemple, une charge de moyenne durée en classe de service 1 ou 2).
  • Coefficient partiel de sécurité (\(\gamma_M\)) : Ce coefficient est appliqué pour obtenir une valeur de calcul (\(f_d\)) à partir de la valeur caractéristique modifiée. Il vise à couvrir diverses incertitudes :
    • Variabilité des propriétés du matériau bois, même au sein d'une même classe.
    • Imperfections géométriques des éléments.
    • Incertitudes dans le modèle de calcul de la résistance.
    • Conséquences d'une éventuelle défaillance.
    En divisant par \(\gamma_M\) (qui est supérieur à 1.0, ici 1.3), on obtient une résistance de calcul plus faible que la résistance caractéristique, ce qui introduit une marge de sécurité dans le dimensionnement.

En résumé, \(k_{mod}\) adapte la résistance aux conditions d'utilisation réelles, et \(\gamma_M\) introduit une marge de sécurité pour tenir compte des incertitudes et assurer la fiabilité de la structure.

Résultat Question 6 : \(k_{mod}\) ajuste la résistance du bois aux conditions d'humidité et de durée de charge, tandis que \(\gamma_M\) est un coefficient de sécurité qui réduit la résistance caractéristique pour obtenir une valeur de calcul sûre.

Quiz Rapide : Testez vos connaissances !

1. Que représente la résistance caractéristique \(f_{m,k}\) du bois ?

2. Si une charge est de très courte durée (ex: impact), le coefficient \(k_{mod}\) sera généralement :

3. Le coefficient partiel de sécurité \(\gamma_M\) pour le bois :

Glossaire

Caractéristiques Mécaniques
Propriétés d'un matériau qui décrivent son comportement sous l'action de forces (ex: résistance, rigidité).
Résistance Caractéristique (\(f_k\))
Valeur d'une propriété de résistance d'un matériau qui correspond à un fractile spécifié (généralement 5%) de la distribution statistique de cette propriété.
Résistance de Calcul (\(f_d\))
Valeur de la résistance d'un matériau utilisée dans les calculs de dimensionnement à l'ELU. Elle est obtenue en divisant la résistance caractéristique par un coefficient partiel de sécurité (\(\gamma_M\)) et en appliquant des coefficients de modification (\(k_{mod}\), etc.).
Module d'Élasticité (\(E\))
Mesure de la rigidité d'un matériau, c'est-à-dire sa capacité à résister à la déformation élastique.
Coefficient de Modification (\(k_{mod}\))
Coefficient qui ajuste les valeurs de résistance du bois pour tenir compte de l'effet de la durée de la charge et de la classe de service (conditions d'humidité).
Coefficient Partiel de Sécurité (\(\gamma_M\))
Coefficient appliqué à la résistance caractéristique d'un matériau pour obtenir sa résistance de calcul. Il couvre les incertitudes sur les propriétés du matériau et les écarts dimensionnels.
Classe de Résistance (Bois)
Classification du bois (ex: C18, C24, GL28h pour le lamellé-collé) basée sur ses propriétés mécaniques caractéristiques (résistance en flexion, module d'élasticité, etc.).
Classe de Service
Classification des conditions d'humidité ambiante dans lesquelles le bois sera utilisé (Classe 1 : sec, Classe 2 : humide, Classe 3 : extérieur exposé).
Classe de Durée de Charge
Classification de la durée pendant laquelle une charge est appliquée (ex: permanente, longue, moyenne, courte, instantanée).
Caractéristiques Mécaniques du Bois - Exercice d'Application

D’autres exercices de structure en bois :

1 Commentaire
  1. Cédrick Sinclairino BOUCKA KOMBILA
    Cédrick Sinclairino BOUCKA KOMBILA sur 24 janvier 2025 à 8h16

    Bonjour, comment faire pour obtenir un livre sur les calculs des contraintes du bois ?
    Les documents sont très instructifs

    Réponse
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *