Études de cas pratique

EGC

Calcul de pente en topographie

Calcul de Pente en Topographie

Calcul de Pente en Topographie

Comprendre le Calcul de Pente en Topographie

La pente topographique est une mesure de l'inclinaison d'un terrain par rapport à l'horizontale. Elle est une donnée fondamentale en topographie, en géographie, en ingénierie civile (routes, voies ferrées, canalisations), en agriculture (drainage, irrigation), en aménagement du territoire et dans de nombreuses autres disciplines. La pente peut être exprimée de plusieurs manières : en pourcentage (%), en degrés (°), en radians, ou sous forme de rapport (par exemple, 1:X ou X pour 1). Le calcul de la pente nécessite généralement de connaître la différence d'altitude (dénivelée) entre deux points et la distance horizontale qui les sépare.

Données de l'étude

On souhaite déterminer la pente d'un terrain entre deux points A et B.

Coordonnées et mesures :

  • Point A :
    • Altitude (\(Z_{\text{A}}\)) : \(125.50 \, \text{m}\)
  • Point B :
    • Altitude (\(Z_{\text{B}}\)) : \(137.20 \, \text{m}\)
  • Distance horizontale entre A et B (\(D_{\text{h}}\)) : \(235.75 \, \text{m}\)

Hypothèses :

  • Les mesures d'altitude et de distance sont précises.
  • Le terrain présente une pente régulière entre les points A et B.

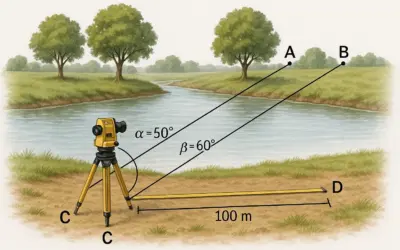
Schéma : Calcul de pente entre deux points
{/* */} {/* */} Point A (ZA) Point B (ZB) {/* */} {/* */} {/* */} {/* */} \(\alpha\) {/* */} {/* */} ΔZ {/* */} Dh Illustration de la Pente Topographique

Schéma illustrant la dénivelée (\(\Delta Z\)) et la distance horizontale (\(D_{\text{h}}\)) entre deux points A et B pour le calcul de la pente.

Questions à traiter

  1. Calculer la dénivelée (\(\Delta Z\)) entre les points A et B.
  2. Calculer la pente (\(P\)) en pourcentage (\(\%\)).
  3. Calculer la pente (\(\alpha\)) en degrés (\(^\circ\)).
  4. Exprimer la pente sous forme de rapport 1:X (par exemple, 1 pour 20).
  5. Si la distance mesurée sur le terrain (distance suivant la pente, \(D_{\text{p}}\)) entre A et B était de \(236.05 \, \text{m}\), quelle serait la distance horizontale calculée à partir de cette mesure et de la dénivelée ? Commenter la différence par rapport à la \(D_{\text{h}}\) donnée.

Correction : Calcul de Pente en Topographie

Question 1 : Calcul de la Dénivelée (\(\Delta Z\))

Principe :

La dénivelée (\(\Delta Z\)) est la différence d'altitude entre les deux points considérés.

Formule(s) utilisée(s) :
\[\Delta Z = |Z_{\text{B}} - Z_{\text{A}}|\]

Ou simplement \(Z_{\text{B}} - Z_{\text{A}}\) si l'on s'intéresse au sens de la pente (montante ou descendante de A vers B). Pour la valeur de la pente, on utilise la valeur absolue.

Données spécifiques :
  • Altitude du point A (\(Z_{\text{A}}\)) : \(125.50 \, \text{m}\)
  • Altitude du point B (\(Z_{\text{B}}\)) : \(137.20 \, \text{m}\)
Calcul :
\[ \begin{aligned} \Delta Z &= 137.20 \, \text{m} - 125.50 \, \text{m} \\ &= 11.70 \, \text{m} \end{aligned} \]

Le point B est plus haut que le point A, la pente est montante de A vers B.

Résultat Question 1 : La dénivelée entre les points A et B est \(\Delta Z = 11.70 \, \text{m}\).

Question 2 : Calcul de la Pente (\(P\)) en Pourcentage (%)

Principe :

La pente en pourcentage est le rapport de la dénivelée (\(\Delta Z\)) à la distance horizontale (\(D_{\text{h}}\)), multiplié par 100.

Formule(s) utilisée(s) :
\[P (\%) = \frac{\Delta Z}{D_{\text{h}}} \times 100\]
Données spécifiques :
  • Dénivelée (\(\Delta Z\)) : \(11.70 \, \text{m}\)
  • Distance horizontale (\(D_{\text{h}}\)) : \(235.75 \, \text{m}\)
Calcul :
\[ \begin{aligned} P (\%) &= \frac{11.70 \, \text{m}}{235.75 \, \text{m}} \times 100 \\ &\approx 0.0496288 \times 100 \\ &\approx 4.96288 \% \end{aligned} \]

Arrondi à deux décimales : \(4.96 \%\).

Résultat Question 2 : La pente entre les points A et B est d'environ \(4.96 \%\).

Question 3 : Calcul de la Pente (\(\alpha\)) en Degrés (\(^\circ\))

Principe :

L'angle de la pente (\(\alpha\)) est l'angle dont la tangente est égale au rapport de la dénivelée à la distance horizontale. \(\tan(\alpha) = \frac{\Delta Z}{D_{\text{h}}}\).

Formule(s) utilisée(s) :
\[\alpha = \arctan\left(\frac{\Delta Z}{D_{\text{h}}}\right)\]

La fonction \(\arctan\) donne un résultat en radians, qu'il faut convertir en degrés si nécessaire (\(1 \, \text{radian} = \frac{180}{\pi} \, \text{degrés}\)). La plupart des calculatrices peuvent donner directement le résultat en degrés.

Données spécifiques :
  • \(\frac{\Delta Z}{D_{\text{h}}} \approx 0.0496288\) (valeur de la pente avant multiplication par 100)
Calcul :
\[ \begin{aligned} \alpha &= \arctan(0.0496288) \\ &\approx 2.8415^\circ \end{aligned} \]

Arrondi à deux décimales : \(2.84^\circ\).

Résultat Question 3 : L'angle de la pente est d'environ \(2.84^\circ\).

Quiz Intermédiaire 1 : Une pente de 100% correspond à un angle de :

Question 4 : Expression de la Pente sous Forme de Rapport 1:X

Principe :

La pente sous forme de rapport 1:X signifie que pour X unités de distance horizontale, on a 1 unité de dénivelée. Donc, \(X = \frac{D_{\text{h}}}{\Delta Z}\).

Formule(s) utilisée(s) :
\[X = \frac{D_{\text{h}}}{\Delta Z}\]
Données spécifiques :
  • Dénivelée (\(\Delta Z\)) : \(11.70 \, \text{m}\)
  • Distance horizontale (\(D_{\text{h}}\)) : \(235.75 \, \text{m}\)
Calcul :
\[ \begin{aligned} X &= \frac{235.75 \, \text{m}}{11.70 \, \text{m}} \\ &\approx 20.14957 \end{aligned} \]

Le rapport est donc approximativement 1:20.15.

Résultat Question 4 : La pente exprimée sous forme de rapport est approximativement 1:20.15.

Question 5 : Distance Horizontale à partir de la Distance Suivant la Pente

Principe :

Si l'on connaît la distance suivant la pente (\(D_{\text{p}}\)) et la dénivelée (\(\Delta Z\)), la distance horizontale (\(D_{\text{h}}\)) peut être calculée en utilisant le théorème de Pythagore : \(D_{\text{p}}^2 = D_{\text{h}}^2 + \Delta Z^2\).

Formule(s) utilisée(s) :
\[D_{\text{h}} = \sqrt{D_{\text{p}}^2 - \Delta Z^2}\]
Données spécifiques :
  • Distance suivant la pente (\(D_{\text{p}}\)) : \(236.05 \, \text{m}\)
  • Dénivelée (\(\Delta Z\)) : \(11.70 \, \text{m}\)
Calcul :
\[ \begin{aligned} D_{\text{h}} &= \sqrt{(236.05 \, \text{m})^2 - (11.70 \, \text{m})^2} \\ &= \sqrt{55719.6025 \, \text{m}^2 - 136.89 \, \text{m}^2} \\ &= \sqrt{55582.7125 \, \text{m}^2} \\ &\approx 235.7597 \, \text{m} \end{aligned} \]
Commentaire :

La distance horizontale calculée (\( \approx 235.76 \, \text{m}\)) est très proche de la distance horizontale donnée initialement (\(235.75 \, \text{m}\)). La petite différence (\(0.01 \, \text{m}\)) peut être due aux arrondis ou à une légère variation dans la mesure de la distance suivant la pente. Cela confirme la cohérence des données pour une pente relativement faible. Pour des pentes fortes, la différence entre \(D_{\text{p}}\) et \(D_{\text{h}}\) serait plus significative.

Résultat Question 5 : La distance horizontale calculée à partir de \(D_{\text{p}}\) et \(\Delta Z\) est d'environ \(235.76 \, \text{m}\). Cette valeur est cohérente avec la \(D_{\text{h}}\) fournie.

Quiz Intermédiaire 2 : La distance suivant la pente (\(D_{\text{p}}\)) est toujours :

Quiz Rapide : Testez vos connaissances (Récapitulatif)

1. Une pente de 5% signifie :

2. La dénivelée est :

3. Pour calculer l'angle d'une pente en degrés à partir de la dénivelée (\(\Delta Z\)) et de la distance horizontale (\(D_{\text{h}}\)), on utilise :

Glossaire

Pente Topographique
Mesure de l'inclinaison d'une surface terrestre par rapport à l'horizontale. Elle indique la raideur du terrain.
Dénivelée (\(\Delta Z\))
Différence d'altitude (ou de hauteur) entre deux points. C'est la composante verticale de la pente.
Distance Horizontale (\(D_{\text{h}}\))
Distance entre deux points mesurée sur un plan horizontal. C'est la projection de la distance réelle sur l'horizontale.
Distance Suivant la Pente (\(D_{\text{p}}\))
Distance réelle mesurée sur la surface du terrain entre deux points, en suivant l'inclinaison naturelle.
Pente en Pourcentage (%)
Exprime la dénivelée pour 100 unités de distance horizontale. Calculée par \((\Delta Z / D_{\text{h}}) \times 100\).
Pente en Degrés (\(^\circ\))
Angle formé par la surface du terrain et le plan horizontal. Calculé par \(\alpha = \arctan(\Delta Z / D_{\text{h}})\).
Pente en Rapport (1:X)
Exprime que pour X unités de distance horizontale, il y a 1 unité de dénivelée. \(X = D_{\text{h}} / \Delta Z\).
Altitude (Z)
Hauteur d'un point par rapport à un niveau de référence donné (souvent le niveau moyen de la mer).
Calcul de Pente en Topographie - Exercice d'Application

D’autres exercices de Topographie:

0 commentaires
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *