Calcul des Coordonnées d’un Point en Topographie
Comprendre le Calcul des Coordonnées
Le calcul des coordonnées planimétriques (X, Y) d'un point est une tâche fondamentale en topographie. Il permet de localiser précisément des objets ou des limites sur le terrain par rapport à un système de référence. Une des méthodes les plus directes est le calcul à partir d'un point connu (station), d'une direction de référence orientée (gisement de référence), d'un angle horizontal mesuré vers le nouveau point, et de la distance horizontale entre la station et ce nouveau point. Ce processus est à la base de la méthode de rayonnement, largement utilisée pour les levés de détails.
Données de l'étude
- \(X_{\text{S}} = 500.000 \, \text{m}\)
- \(Y_{\text{S}} = 1000.000 \, \text{m}\)
- \(X_{\text{R0}} = 580.000 \, \text{m}\)
- \(Y_{\text{R0}} = 1060.000 \, \text{m}\)
- Angle horizontal lu (\(L_H\)) depuis la direction SR0 vers SP (sens horaire) : \(75.5020^\circ\)
- Distance horizontale (\(D_{H,SP}\)) de S à P : \(125.320 \, \text{m}\)
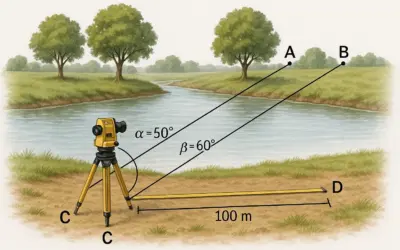
Schéma : Calcul de Coordonnées par Rayonnement
Schéma illustrant le calcul des coordonnées du point P depuis la station S, orientée sur R0.
Questions à traiter
- Expliquer le principe du calcul de coordonnées planimétriques d'un point à partir d'un point connu, d'un gisement et d'une distance.
- Calculer le gisement de la direction de référence SR0 (\(G_{\text{SR0}}\)).
- Calculer le gisement de la visée SP (\(G_{\text{SP}}\)).
- Calculer les déports en X (\(\Delta X_{\text{SP}}\)) et en Y (\(\Delta Y_{\text{SP}}\)) entre S et P.
- Calculer les coordonnées du point P (\(X_{\text{P}}, Y_{\text{P}}\)).
- Un deuxième point Q a pour coordonnées \(X_{\text{Q}} = 650.123 \, \text{m}\) et \(Y_{\text{Q}} = 1085.456 \, \text{m}\). Calculer la distance entre les points P et Q.
Correction : Calcul des Coordonnées d’un Point
Question 1 : Principe du calcul de coordonnées par gisement et distance
Principe :
Le calcul de coordonnées planimétriques (X, Y) d'un nouveau point P à partir d'un point connu S (la station) est une application directe de la trigonométrie en coordonnées polaires. Il nécessite :
À partir de ces éléments, on calcule les déports (ou accroissements de coordonnées) \(\Delta X_{\text{SP}}\) et \(\Delta Y_{\text{SP}}\). Ces déports représentent les composantes du vecteur SP selon les axes X (Est) et Y (Nord) du système de coordonnées.
Les formules pour les déports sont :
Ensuite, les coordonnées du point P sont obtenues en ajoutant ces déports aux coordonnées de la station S :
Il est crucial que le gisement \(G_{\text{SP}}\) soit correctement déterminé et que les fonctions trigonométriques utilisent l'angle dans l'unité appropriée (généralement radians pour les calculatrices et langages de programmation, bien que les gisements soient souvent exprimés en degrés, grades ou millièmes en topographie).
Question 2 : Gisement de la direction de référence SR0 (\(G_{\text{SR0}}\))
Principe :
Le gisement d'une ligne entre deux points connus (S et R0) est calculé à partir de leurs coordonnées cartésiennes en utilisant la fonction arc tangente.
Formule(s) utilisée(s) :
La fonction \(\text{atan2}(\Delta X, \Delta Y)\) donne un résultat en radians, qu'il faut convertir en degrés et ajuster pour être entre \(0^\circ\) et \(360^\circ\).
Données spécifiques :
- \(X_{\text{S}} = 500.000 \, \text{m}\), \(Y_{\text{S}} = 1000.000 \, \text{m}\)
- \(X_{\text{R0}} = 580.000 \, \text{m}\), \(Y_{\text{R0}} = 1060.000 \, \text{m}\)
Calcul :
Conversion en degrés :
Comme \(\Delta X > 0\) et \(\Delta Y > 0\), le gisement est dans le premier quadrant.
Question 3 : Gisement de la visée SP (\(G_{\text{SP}}\))
Principe :
Le gisement de la visée SP est obtenu en ajoutant l'angle horizontal lu (\(L_H\)) vers P (mesuré dans le sens horaire par rapport à la référence SR0) au gisement de la référence (\(G_{\text{SR0}}\)).
Formule(s) utilisée(s) :
Données spécifiques :
- \(G_{\text{SR0}} \approx 53.1301^\circ\)
- \(L_H = 75.5020^\circ\)
Calcul :
Quiz Intermédiaire 1 : Si l'angle horizontal \(L_H\) était mesuré dans le sens antihoraire, comment calculerait-on \(G_{\text{SP}}\) ?
Question 4 : Calcul des déports \(\Delta X_{\text{SP}}\) et \(\Delta Y_{\text{SP}}\)
Principe :
Les déports sont les projections de la distance horizontale sur les axes X et Y, calculées à l'aide du gisement de la visée.
Formule(s) utilisée(s) :
Données spécifiques :
- \(D_{H,SP} = 125.320 \, \text{m}\)
- \(G_{\text{SP}} \approx 128.6321^\circ\)
Calcul :
Question 5 : Coordonnées du point P (\(X_{\text{P}}, Y_{\text{P}}\))
Principe :
Les coordonnées du point P sont obtenues en ajoutant les déports calculés aux coordonnées de la station S.
Formule(s) utilisée(s) :
Données spécifiques :
- \(X_{\text{S}} = 500.000 \, \text{m}\), \(Y_{\text{S}} = 1000.000 \, \text{m}\)
- \(\Delta X_{\text{SP}} \approx +97.898 \, \text{m}\)
- \(\Delta Y_{\text{SP}} \approx -78.238 \, \text{m}\)
Calcul :
Question 6 : Distance entre les points P et Q
Principe :
La distance entre deux points P(\(X_{\text{P}}, Y_{\text{P}}\)) et Q(\(X_{\text{Q}}, Y_{\text{Q}}\)) est calculée en utilisant la formule de la distance euclidienne.
Formule(s) utilisée(s) :
Données spécifiques :
- \(X_{\text{P}} \approx 597.898 \, \text{m}\), \(Y_{\text{P}} \approx 921.762 \, \text{m}\)
- \(X_{\text{Q}} = 650.123 \, \text{m}\), \(Y_{\text{Q}} = 1085.456 \, \text{m}\)
Calcul :
Quiz Intermédiaire 2 : Si les coordonnées de P étaient identiques à celles de Q, la distance PQ serait :
Quiz Rapide : Testez vos connaissances (Récapitulatif)
7. Le calcul des coordonnées \(X_P = X_S + D_H \cdot \sin(G_{SP})\) est correct si le gisement \(G_{SP}\) est :
8. Si le gisement d'une ligne AB est de \(270^\circ\), cela signifie que B est situé :
9. En topographie, la fonction \(\text{atan2}(\Delta X, \Delta Y)\) est souvent utilisée pour calculer un gisement car :
Glossaire
- Coordonnées Planimétriques (X, Y)
- Couple de valeurs numériques qui définissent la position d'un point sur un plan horizontal par rapport à un système de référence (axes X et Y, souvent Est et Nord).
- Gisement (ou Azimuth)
- Angle horizontal mesuré dans le sens horaire à partir d'une direction de référence (généralement le Nord géographique ou de la projection cartographique) jusqu'à une ligne ou une direction donnée. Varie de \(0^\circ\) à \(360^\circ\).
- Distance Horizontale (\(D_H\))
- Distance entre deux points, réduite au plan horizontal. C'est la distance qui serait mesurée si le terrain était parfaitement plat entre les deux points.
- Rayonnement (Levé par)
- Méthode de levé topographique consistant à déterminer la position de points par mesure d'un angle horizontal et d'une distance horizontale à partir d'une station connue et orientée.
- Point de Station (S)
- Point sur lequel l'instrument topographique (théodolite, station totale) est installé pour effectuer des mesures.
- Référence (Orientation)
- Direction connue (par exemple vers un autre point connu ou le Nord) utilisée pour orienter l'instrument à la station et servir d'origine aux mesures angulaires.
- Déports (\(\Delta X, \Delta Y\))
- Différences de coordonnées entre deux points selon les axes X et Y. \(\Delta X = X_{\text{final}} - X_{\text{initial}}\), \(\Delta Y = Y_{\text{final}} - Y_{\text{initial}}\).
- atan2(y, x)
- Fonction mathématique qui calcule l'arc tangente de \(y/x\) en utilisant les signes des deux arguments pour déterminer le quadrant correct de l'angle résultant (généralement entre \(-\pi\) et \(\pi\) radians).
D’autres exercices de topographie:






0 commentaires