Études de cas pratique

EGC

Vérification d’une poutre métallique

Vérification d’une Poutre métallique

Vérification d’une Poutre métallique

Comprendre la Vérification d’une Poutre métallique

Les charpentes métalliques sont largement utilisées dans la construction pour leur résistance, leur légèreté relative et leur capacité à franchir de grandes portées. Le dimensionnement des éléments d'une charpente métallique, comme les poutres (pannes, traverses, etc.) et les poteaux, implique de s'assurer qu'ils peuvent résister aux sollicitations (charges permanentes, d'exploitation, climatiques) sans dépasser les limites de résistance du matériau (État Limite Ultime - ELU) et sans présenter de déformations excessives (État Limite de Service - ELS). Cet exercice se concentre sur la vérification à l'ELU d'une poutre en acier soumise à la flexion et au cisaillement.

Données de l'étude

On étudie une poutre en acier (profilé IPE), simplement appuyée, utilisée comme traverse dans une structure métallique.

Caractéristiques géométriques et matériaux :

  • Profilé choisi : IPE 300
  • Portée de la poutre entre appuis (\(L\)) : \(7.0 \, \text{m}\)
  • Acier : S275 (\(f_y = 275 \, \text{MPa}\))
  • Coefficient partiel de sécurité pour la résistance des sections (\(\gamma_{M0}\)) : \(1.0\)
  • Caractéristiques du profilé IPE 300 (extrait d'un catalogue) :
    • Aire de la section (\(A\)) : \(53.8 \, \text{cm}^2\)
    • Module d'inertie plastique par rapport à l'axe fort (\(W_{pl,y}\)) : \(628.4 \, \text{cm}^3\)
    • Aire de cisaillement (\(A_v\)) : \(29.1 \, \text{cm}^2\) (valeur typique pour IPE 300, à vérifier pour un calcul précis).

Charges caractéristiques :

  • Charge permanente linéique (incluant poids propre estimé de la poutre et des éléments supportés) : \(g_k = 5.0 \, \text{kN/m}\)
  • Charge d'exploitation linéique (catégorie B - bureaux) : \(q_k = 8.0 \, \text{kN/m}\)
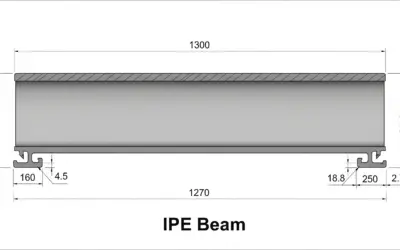
Schéma : Poutre en Acier IPE et Charges
Poutre en flexion q_Ed L = 7.0 m Section IPE 300 b (IPE300) h (IPE300)

Poutre IPE simplement appuyée avec charge répartie et sa section transversale.

Questions à traiter

  1. Calculer la charge totale linéique pondérée à l'ELU (\(q_{Ed,tot}\)) sur la poutre.
  2. Calculer le moment fléchissant maximal de calcul (\(M_{Ed}\)) et l'effort tranchant maximal de calcul (\(V_{Ed}\)) dans la poutre.
  3. Calculer la résistance de calcul de l'acier en traction/compression (\(f_{yd}\)).
  4. Calculer le moment résistant plastique de la section (\(M_{pl,Rd}\)).
  5. Vérifier la résistance de la poutre en flexion (\(M_{Ed} \leq M_{pl,Rd}\)).
  6. Calculer la résistance de calcul au cisaillement (\(V_{pl,Rd}\)).
  7. Vérifier la résistance de la poutre au cisaillement (\(V_{Ed} \leq V_{pl,Rd}\)).
  8. Vérifier si une interaction flexion-cisaillement doit être considérée (\(V_{Ed} > 0.5 V_{pl,Rd}\)).

Correction : Vérification d’une Poutre métallique

Question 1 : Charge Totale Linéique Pondérée à l'ELU (\(q_{Ed,tot}\))

Principe :

Pour assurer la sécurité de la structure, on majore les charges caractéristiques (valeurs statistiques) par des coefficients de sécurité pour obtenir les charges de calcul à l'État Limite Ultime (ELU). La combinaison la plus courante pour les charges permanentes (\(g_k\)) et une seule charge d'exploitation variable (\(q_k\)) est \(1.35 G_k + 1.5 Q_k\).

Formule(s) utilisée(s) :
\[q_{Ed,tot} = 1.35 g_k + 1.5 q_k\]
Données spécifiques :
  • Charge permanente caractéristique (\(g_k\)) : \(5.0 \, \text{kN/m}\)
  • Charge d'exploitation caractéristique (\(q_k\)) : \(8.0 \, \text{kN/m}\)
Calcul :
\[ \begin{aligned} q_{Ed,tot} &= (1.35 \times 5.0 \, \text{kN/m}) + (1.5 \times 8.0 \, \text{kN/m}) \\ &= 6.75 \, \text{kN/m} + 12.0 \, \text{kN/m} \\ &= 18.75 \, \text{kN/m} \end{aligned} \]
Résultat Question 1 : La charge totale linéique pondérée à l'ELU est \(q_{Ed,tot} = 18.75 \, \text{kN/m}\).

Question 2 : Moment (\(M_{Ed}\)) et Effort Tranchant (\(V_{Ed}\)) Maximaux

Principe :

Pour une poutre simplement appuyée (c'est-à-dire reposant librement sur deux appuis) de portée \(L\) et soumise à une charge uniformément répartie \(q_{Ed,tot}\), le moment fléchissant est maximal au milieu de la portée. Cet effort tend à courber la poutre. L'effort tranchant est maximal aux appuis et représente les forces tendant à "couper" la poutre verticalement.

Formule(s) utilisée(s) :
\[M_{Ed,max} = \frac{q_{Ed,tot} L^2}{8}\] \[V_{Ed,max} = \frac{q_{Ed,tot} L}{2}\]
Données spécifiques :
  • \(q_{Ed,tot} = 18.75 \, \text{kN/m}\)
  • Portée (\(L\)) : \(7.0 \, \text{m}\)
Calcul :
\[ \begin{aligned} M_{Ed,max} &= \frac{18.75 \, \text{kN/m} \times (7.0 \, \text{m})^2}{8} \\ &= \frac{18.75 \times 49}{8} \, \text{kN} \cdot \text{m} \\ &= \frac{918.75}{8} \, \text{kN} \cdot \text{m} \\ &\approx 114.84 \, \text{kN} \cdot \text{m} \end{aligned} \]
\[ \begin{aligned} V_{Ed,max} &= \frac{18.75 \, \text{kN/m} \times 7.0 \, \text{m}}{2} \\ &= \frac{131.25}{2} \, \text{kN} \\ &= 65.625 \, \text{kN} \end{aligned} \]
Résultat Question 2 : \(M_{Ed,max} \approx 114.84 \, \text{kN} \cdot \text{m}\) et \(V_{Ed,max} = 65.625 \, \text{kN}\).

Quiz Intermédiaire 1 : Si la portée L de la poutre double, le moment fléchissant maximal \(M_{Ed,max}\) (pour une même charge \(q_{Ed,tot}\)) :

Question 3 : Résistance de Calcul de l'Acier (\(f_{yd}\))

Principe :

La résistance de calcul de l'acier (\(f_{yd}\)) est la valeur de la limite d'élasticité caractéristique (\(f_y\)) divisée par le coefficient partiel de sécurité pour la résistance des sections (\(\gamma_{M0}\)). C'est la contrainte maximale que l'acier peut atteindre en service à l'ELU avant de plastifier de manière significative.

Formule(s) utilisée(s) :
\[f_{yd} = \frac{f_y}{\gamma_{M0}}\]
Données spécifiques :
  • Limite d'élasticité de l'acier S275 (\(f_y\)) : \(275 \, \text{MPa}\)
  • Coefficient partiel de sécurité (\(\gamma_{M0}\)) : \(1.0\)
Calcul :
\[ \begin{aligned} f_{yd} &= \frac{275 \, \text{MPa}}{1.0} \\ &= 275 \, \text{MPa} \, (\text{ou N/mm}^2) \end{aligned} \]
Résultat Question 3 : La résistance de calcul de l'acier est \(f_{yd} = 275 \, \text{MPa}\).

Question 4 : Moment Résistant Plastique (\(M_{pl,Rd}\))

Principe :

Pour les profilés en acier de classe 1 ou 2 (capables de développer des déformations plastiques importantes sans instabilité locale), la résistance en flexion à l'ELU est calculée en utilisant le module de section plastique (\(W_{pl,y}\)). Le moment résistant plastique est le produit de ce module par la résistance de calcul de l'acier (\(f_{yd}\)).

Formule(s) utilisée(s) (Eurocode 3) :
\[M_{pl,Rd} = W_{pl,y} \cdot f_{yd}\]

(Puisque \(\gamma_{M0}=1.0\), \(M_{pl,Rd} = W_{pl,y} \cdot f_y\))

Données spécifiques (convertir les unités pour la cohérence) :
  • Profilé IPE 300 : \(W_{pl,y} = 628.4 \, \text{cm}^3 = 628.4 \times 10^3 \, \text{mm}^3\)
  • \(f_{yd} = 275 \, \text{N/mm}^2\)
Calcul :
\[ \begin{aligned} M_{pl,Rd} &= (628.4 \times 10^3 \, \text{mm}^3) \times (275 \, \text{N/mm}^2) \\ &= 172810000 \, \text{N} \cdot \text{mm} \end{aligned} \]

Conversion en kN·m :

\[ M_{pl,Rd} = \frac{172810000}{10^6} \, \text{kN} \cdot \text{m} \approx 172.81 \, \text{kN} \cdot \text{m} \]
Résultat Question 4 : Le moment résistant plastique du profilé IPE 300 est \(M_{pl,Rd} \approx 172.81 \, \text{kN} \cdot \text{m}\).

Question 5 : Vérification de la Résistance en Flexion

Principe :

La poutre est considérée comme suffisamment résistante en flexion si le moment fléchissant de calcul agissant (\(M_{Ed}\)) est inférieur ou égal au moment résistant plastique de calcul de la section (\(M_{pl,Rd}\)).

Formule(s) utilisée(s) :
\[M_{Ed} \leq M_{pl,Rd}\]
Données spécifiques :
  • \(M_{Ed} \approx 114.84 \, \text{kN} \cdot \text{m}\)
  • \(M_{pl,Rd} \approx 172.81 \, \text{kN} \cdot \text{m}\)
Comparaison :
\[114.84 \, \text{kN} \cdot \text{m} \leq 172.81 \, \text{kN} \cdot \text{m} \quad (\text{OK})\]

La condition est vérifiée. Le rapport d'utilisation est \(114.84 / 172.81 \approx 0.66 < 1.0\).

Résultat Question 5 : La poutre IPE 300 résiste en flexion.

Quiz Intermédiaire 2 : Si le moment agissant \(M_{Ed}\) était de \(180 \, \text{kN} \cdot \text{m}\), la poutre IPE 300 serait-elle adéquate en flexion ?

Question 6 : Résistance de Calcul au Cisaillement (\(V_{pl,Rd}\))

Principe :

La résistance de calcul au cisaillement d'une section en acier (\(V_{pl,Rd}\)) est basée sur la plastification de l'aire de cisaillement (\(A_v\)). La contrainte de cisaillement limite est typiquement prise comme \(f_y / \sqrt{3}\) (selon le critère de von Mises), et on divise par le coefficient partiel de sécurité \(\gamma_{M0}\).

Formule(s) utilisée(s) (Eurocode 3) :
\[V_{pl,Rd} = \frac{A_v \cdot (f_y / \sqrt{3})}{\gamma_{M0}}\]
Données spécifiques (convertir les unités si nécessaire) :
  • Aire de cisaillement (\(A_v\)) : \(29.1 \, \text{cm}^2 = 2910 \, \text{mm}^2\)
  • \(f_y = 275 \, \text{MPa} = 275 \, \text{N/mm}^2\)
  • \(\gamma_{M0} = 1.0\)
Calcul :
\[ \begin{aligned} V_{pl,Rd} &= \frac{2910 \, \text{mm}^2 \times (275 \, \text{N/mm}^2 / \sqrt{3})}{1.0} \\ &\approx \frac{2910 \times (275 / 1.73205)}{1.0} \, \text{N} \\ &\approx \frac{2910 \times 158.77}{1.0} \, \text{N} \\ &\approx 461910.7 \, \text{N} \end{aligned} \]

Conversion en kN :

\[ V_{pl,Rd} \approx 461.91 \, \text{kN} \]
Résultat Question 6 : La résistance de calcul au cisaillement est \(V_{pl,Rd} \approx 461.91 \, \text{kN}\).

Question 7 : Vérification de la Résistance au Cisaillement

Principe :

La poutre est considérée comme suffisamment résistante au cisaillement si l'effort tranchant de calcul agissant (\(V_{Ed}\)) est inférieur ou égal à l'effort tranchant résistant de calcul (\(V_{pl,Rd}\)).

Formule(s) utilisée(s) :
\[V_{Ed} \leq V_{pl,Rd}\]
Données spécifiques :
  • \(V_{Ed} = 65.625 \, \text{kN}\)
  • \(V_{pl,Rd} \approx 461.91 \, \text{kN}\)
Comparaison :
\[65.625 \, \text{kN} \leq 461.91 \, \text{kN} \quad (\text{OK})\]

La condition est vérifiée.

Résultat Question 7 : La poutre IPE 300 résiste au cisaillement.

Question 8 : Vérification de la Nécessité d'Interaction Flexion-Cisaillement

Principe :

L'Eurocode 3 stipule que si l'effort tranchant agissant \(V_{Ed}\) est inférieur à 50% de la résistance plastique au cisaillement \(V_{pl,Rd}\), l'effet du cisaillement sur la résistance en moment peut généralement être négligé pour les profilés en I et H doublement symétriques. Si \(V_{Ed} > 0.5 \cdot V_{pl,Rd}\), une vérification d'interaction est requise, car un effort tranchant élevé peut réduire la capacité en flexion.

Formule(s) utilisée(s) :
\[\text{Condition : } V_{Ed} > 0.5 \cdot V_{pl,Rd} \quad ?\]
Données spécifiques :
  • \(V_{Ed} = 65.625 \, \text{kN}\)
  • \(V_{pl,Rd} \approx 461.91 \, \text{kN}\)
Calcul :
\[ 0.5 \cdot V_{pl,Rd} \approx 0.5 \times 461.91 \, \text{kN} \approx 230.96 \, \text{kN} \]

Comparaison :

\[ V_{Ed} = 65.625 \, \text{kN} \leq 0.5 \cdot V_{pl,Rd} = 230.96 \, \text{kN} \]

Puisque \(V_{Ed}\) (65.625 kN) n'est pas supérieur à 50% de \(V_{pl,Rd}\) (230.96 kN), l'effet du cisaillement sur la résistance en moment peut être négligé. Aucune vérification d'interaction flexion-cisaillement n'est requise dans ce cas.

Résultat Question 8 : L'effort tranchant agissant est inférieur à 50% de la résistance au cisaillement. Une vérification d'interaction flexion-cisaillement n'est pas nécessaire.

Quiz Rapide : Testez vos connaissances

1. Qu'est-ce qu'un profilé IPE en charpente métallique ?

2. L'acier S275 a une limite d'élasticité caractéristique (\(f_y\)) de :

3. La vérification à l'ELU pour une poutre en acier sollicitée en flexion implique généralement de s'assurer que :

Glossaire

Charpente Métallique
Structure porteuse d'un bâtiment ou d'un ouvrage, constituée principalement d'éléments en acier (poutres, poteaux, contreventements).
Poutre (Traverse, Panne)
Élément structural linéaire conçu pour résister principalement à la flexion et au cisaillement dus aux charges transversales.
Profilé IPE
Type de profilé en acier en forme de "I" avec des ailes parallèles (Européen), standardisé, utilisé couramment pour les poutres.
Acier S275
Nuance d'acier de construction structural ayant une limite d'élasticité minimale garantie de \(275 \, \text{MPa}\).
État Limite Ultime (ELU)
État limite correspondant à la capacité portante maximale de la structure ou d'un de ses éléments avant rupture ou perte de stabilité.
Moment Fléchissant de Calcul (\(M_{Ed}\))
Moment sollicitant la section, calculé à l'ELU à partir des charges pondérées.
Effort Tranchant de Calcul (\(V_{Ed}\))
Effort tranchant sollicitant la section, calculé à l'ELU.
Module de Section Plastique (\(W_{pl,y}\))
Caractéristique géométrique d'une section utilisée pour calculer le moment de plastification complète de la section.
Résistance de Calcul en Flexion (\(M_{c,Rd}\))
Capacité maximale d'une section à résister à un moment fléchissant à l'ELU, en tenant compte de la plastification si la section le permet.
Aire de Cisaillement (\(A_v\))
Partie de l'aire de la section considérée comme efficace pour reprendre l'effort tranchant (principalement l'âme pour les profilés en I).
Résistance de Calcul au Cisaillement (\(V_{pl,Rd}\))
Capacité maximale d'une section à résister à un effort tranchant à l'ELU, basée sur la plastification en cisaillement.
Coefficient Partiel de Sécurité (\(\gamma_{M0}\))
Coefficient appliqué à la résistance du matériau pour obtenir la résistance de calcul pour la vérification de la résistance des sections.
Vérification d’une Poutre métallique – Exercice d'Application

D’autres exercices de structure métallique:

1 Commentaire
Soumettre un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *